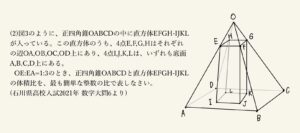
今回は石川県高校入試2021年度数学大問6⑵の別解を紹介します。
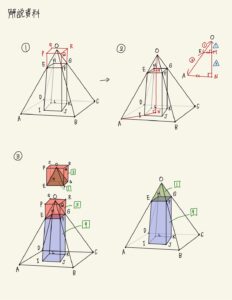
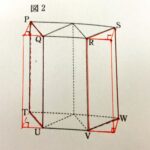
①図のように4点E,F,G,Hを底面とし、高さが正四角推O-EFGHと同じである直方体PQRS-EFGHを考える。
このとき直方体PQRS-EFGHの体積は正四角推O-EFGHの体積の3倍である。
②図のように点Oから平面EFGH,ABCDに向かって下した垂線の足をそれぞれM,Nとする。
このとき△OEM∽△OANであり、OE:EA=1:3であるからOM:MN=1:3である。
③①より正四角推O-EFGH:直方体PQRS-EFGH=1:3、②より直方体PQRS-EFGH:直方体EFGH-IJKL=1:3である。
よって正四角推O-EFGH:直方体EFGH-IJKL=1:9となる。
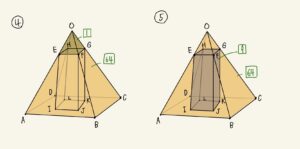
④正四角推O-EFGHと正四角推O-ABCDについて相似比が1:4であるため体積比が1:64となる。
⑤③より正四角推O-EFGH:直方体EFGH-IJKL=1:9
④より正四角推O-EFGH:正四角推O-ABCD=1:64
したがって正四角推O-ABCD:直方体EFGH-IJKL=64:9である。